Spectral vs Finite Difference Convergence¶
Numerical differentiation methods differ dramatically in how quickly they converge to the exact answer as the number of grid points increases. Finite difference methods on equidistant grids achieve algebraic convergence: the error decreases as a power of the grid spacing, \(\mathcal{O}(h^p)\), where \(p\) is the accuracy order. Spectral methods (Chebyshev, FFT) achieve exponential convergence for smooth functions: the error drops faster than any power of \(N\).
The fundamental tradeoff is between method order and grid resolution. A low-order finite difference scheme needs many grid points to achieve high accuracy, while a spectral method can reach machine precision with remarkably few points.
In this notebook, we demonstrate this by computing derivatives of known smooth functions using different axis types in numgrids, and comparing the maximum error as a function of the number of grid points \(N\).
[1]:
import numpy as np
import matplotlib.pyplot as plt
from numgrids import Grid, Diff, AxisType, create_axis
plt.rcParams.update({
'figure.figsize': (10, 6),
'font.size': 12,
'lines.linewidth': 2,
'lines.markersize': 7,
'axes.grid': True,
'grid.alpha': 0.3,
})
Test Function (Non-Periodic)¶
We use the smooth, non-periodic function
on the interval \([-5, 5]\). Its analytical derivative is
[2]:
def f(x):
return np.exp(-x**2) * np.cos(3 * x)
def f_prime(x):
return np.exp(-x**2) * (-2 * x * np.cos(3 * x) - 3 * np.sin(3 * x))
# Quick plot of the test function and its derivative
x_fine = np.linspace(-5, 5, 500)
fig, (ax1, ax2) = plt.subplots(1, 2, figsize=(12, 4))
ax1.plot(x_fine, f(x_fine), 'k-')
ax1.set_title(r"$f(x) = e^{-x^2} \cos(3x)$")
ax1.set_xlabel("x")
ax2.plot(x_fine, f_prime(x_fine), 'k-')
ax2.set_title(r"$f'(x) = e^{-x^2}(-2x\cos(3x) - 3\sin(3x))$")
ax2.set_xlabel("x")
plt.tight_layout()
plt.show()
Non-Periodic Convergence Study¶
We compare four differentiation approaches:
Equidistant finite differences with accuracy orders 2, 4, and 6
Chebyshev spectral differentiation
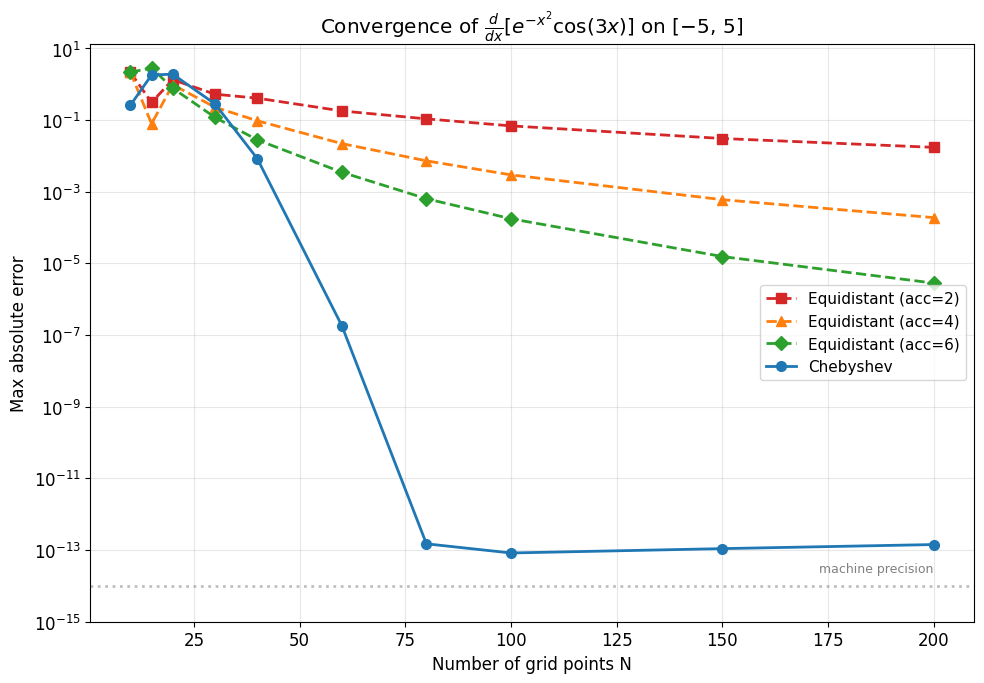
For each method and each value of \(N\), we create a 1D grid on \([-5, 5]\), compute the numerical first derivative, and measure the maximum absolute error against the analytical derivative.
[3]:
Ns = [10, 15, 20, 30, 40, 60, 80, 100, 150, 200]
errors = {
"Equidistant (acc=2)": [],
"Equidistant (acc=4)": [],
"Equidistant (acc=6)": [],
"Chebyshev": [],
}
for N in Ns:
# Equidistant finite differences with different accuracy orders
for acc in [2, 4, 6]:
grid = Grid(create_axis(AxisType.EQUIDISTANT, N, -5, 5))
x = grid.coords
df = Diff(grid, 1, 0, acc=acc)(f(x))
err = np.max(np.abs(df - f_prime(x)))
errors[f"Equidistant (acc={acc})"].append(err)
# Chebyshev spectral
grid = Grid(create_axis(AxisType.CHEBYSHEV, N, -5, 5))
x = grid.coords
df = Diff(grid, 1, 0)(f(x))
err = np.max(np.abs(df - f_prime(x)))
errors["Chebyshev"].append(err)
# Print a summary table
print(f"{'N':>5s} {'FD acc=2':>12s} {'FD acc=4':>12s} {'FD acc=6':>12s} {'Chebyshev':>12s}")
print("-" * 62)
for i, N in enumerate(Ns):
print(f"{N:5d} {errors['Equidistant (acc=2)'][i]:12.3e} "
f"{errors['Equidistant (acc=4)'][i]:12.3e} "
f"{errors['Equidistant (acc=6)'][i]:12.3e} "
f"{errors['Chebyshev'][i]:12.3e}")
N FD acc=2 FD acc=4 FD acc=6 Chebyshev
--------------------------------------------------------------
10 2.155e+00 2.169e+00 2.177e+00 2.605e-01
15 3.124e-01 7.905e-02 2.854e+00 1.817e+00
20 1.344e+00 9.735e-01 7.803e-01 1.916e+00
30 5.287e-01 2.291e-01 1.193e-01 2.838e-01
40 4.103e-01 9.608e-02 2.813e-02 8.442e-03
60 1.804e-01 2.214e-02 3.508e-03 1.826e-07
80 1.084e-01 7.303e-03 6.407e-04 1.494e-13
100 6.914e-02 2.964e-03 1.766e-04 8.293e-14
150 3.068e-02 6.023e-04 1.556e-05 1.097e-13
200 1.737e-02 1.899e-04 2.823e-06 1.426e-13
Plot: Non-Periodic Convergence¶
On a semilogy plot, algebraic convergence (finite differences) shows as a curve that flattens out, while exponential convergence (Chebyshev) shows as a line that drops steeply. The Chebyshev method reaches machine precision (\(\sim 10^{-13}\)) at around \(N = 40\), while finite differences with 200 points are still orders of magnitude less accurate.
[4]:
fig, ax = plt.subplots(figsize=(10, 7))
styles = {
"Equidistant (acc=2)": {"marker": "s", "color": "#d62728", "linestyle": "--"},
"Equidistant (acc=4)": {"marker": "^", "color": "#ff7f0e", "linestyle": "--"},
"Equidistant (acc=6)": {"marker": "D", "color": "#2ca02c", "linestyle": "--"},
"Chebyshev": {"marker": "o", "color": "#1f77b4", "linestyle": "-"},
}
for label, errs in errors.items():
ax.semilogy(Ns, errs, label=label, **styles[label])
ax.set_xlabel("Number of grid points N")
ax.set_ylabel("Max absolute error")
ax.set_title(r"Convergence of $\frac{d}{dx}[e^{-x^2}\cos(3x)]$ on $[-5,\, 5]$")
ax.legend(fontsize=11)
ax.set_ylim(bottom=1e-15)
ax.axhline(y=1e-14, color='gray', linestyle=':', alpha=0.5, label='_nolegend_')
ax.text(Ns[-1], 2e-14, 'machine precision', ha='right', va='bottom',
fontsize=9, color='gray')
plt.tight_layout()
plt.show()
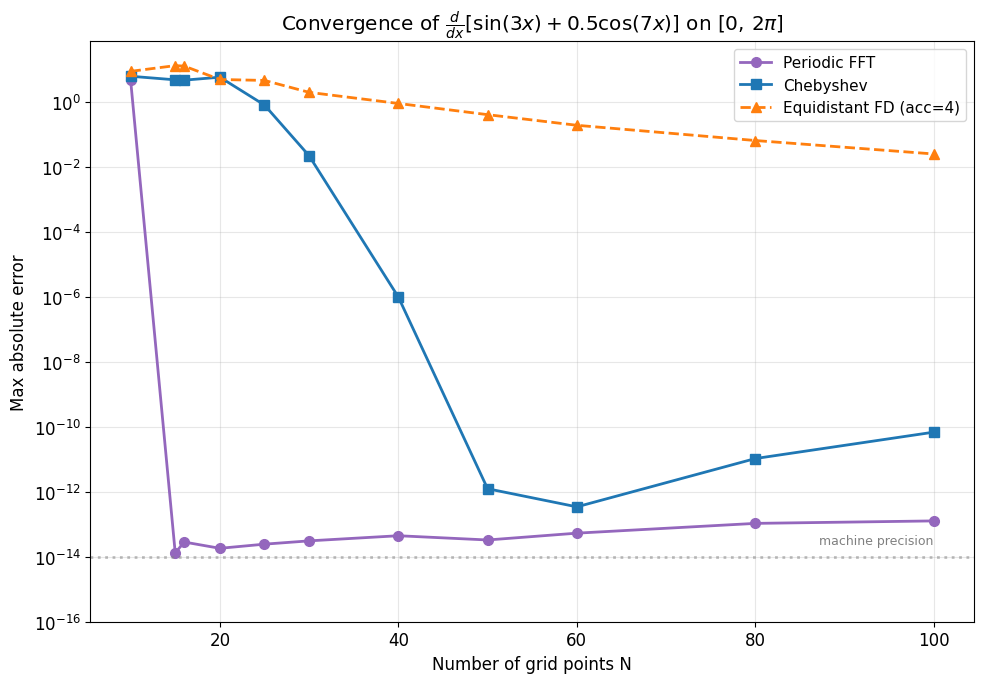
Periodic Function Convergence Study¶
For periodic functions, the natural spectral method is the FFT on an equidistant periodic grid. We compare:
Equidistant periodic (FFT) – spectral method via the discrete Fourier transform
Chebyshev – spectral method for non-periodic domains
Equidistant finite differences (acc=4) – classical FD baseline
Test function:
[5]:
def g(x):
return np.sin(3 * x) + 0.5 * np.cos(7 * x)
def g_prime(x):
return 3 * np.cos(3 * x) - 3.5 * np.sin(7 * x)
Ns_periodic = [10, 15, 16, 20, 25, 30, 40, 50, 60, 80, 100]
errors_periodic = {
"Periodic FFT": [],
"Chebyshev": [],
"Equidistant FD (acc=4)": [],
}
for N in Ns_periodic:
# Periodic FFT (equidistant periodic grid)
grid = Grid(create_axis(AxisType.EQUIDISTANT_PERIODIC, N, 0, 2 * np.pi))
x = grid.coords
df = Diff(grid, 1, 0)(g(x))
err = np.max(np.abs(df - g_prime(x)))
errors_periodic["Periodic FFT"].append(err)
# Chebyshev
grid = Grid(create_axis(AxisType.CHEBYSHEV, N, 0, 2 * np.pi))
x = grid.coords
df = Diff(grid, 1, 0)(g(x))
err = np.max(np.abs(df - g_prime(x)))
errors_periodic["Chebyshev"].append(err)
# Equidistant finite differences
grid = Grid(create_axis(AxisType.EQUIDISTANT, N, 0, 2 * np.pi))
x = grid.coords
df = Diff(grid, 1, 0, acc=4)(g(x))
err = np.max(np.abs(df - g_prime(x)))
errors_periodic["Equidistant FD (acc=4)"].append(err)
Plot: Periodic Convergence¶
For a periodic function on a periodic domain, the FFT spectral method converges the fastest. Once \(N\) exceeds twice the highest frequency in the signal (here, \(N > 14\) suffices for modes up to 7), the FFT derivative becomes exact to machine precision. The Chebyshev method also converges exponentially but slightly slower since it does not exploit the periodicity.
[6]:
fig, ax = plt.subplots(figsize=(10, 7))
styles_periodic = {
"Periodic FFT": {"marker": "o", "color": "#9467bd", "linestyle": "-"},
"Chebyshev": {"marker": "s", "color": "#1f77b4", "linestyle": "-"},
"Equidistant FD (acc=4)": {"marker": "^", "color": "#ff7f0e", "linestyle": "--"},
}
for label, errs in errors_periodic.items():
ax.semilogy(Ns_periodic, errs, label=label, **styles_periodic[label])
ax.set_xlabel("Number of grid points N")
ax.set_ylabel("Max absolute error")
ax.set_title(r"Convergence of $\frac{d}{dx}[\sin(3x) + 0.5\cos(7x)]$ on $[0,\, 2\pi]$")
ax.legend(fontsize=11)
ax.set_ylim(bottom=1e-16)
ax.axhline(y=1e-14, color='gray', linestyle=':', alpha=0.5)
ax.text(Ns_periodic[-1], 2e-14, 'machine precision', ha='right', va='bottom',
fontsize=9, color='gray')
plt.tight_layout()
plt.show()
Visual Comparison at N = 20¶
To see why the numbers above matter in practice, let us compare the numerical derivatives from Equidistant FD (acc=4) and Chebyshev at just \(N = 20\) grid points. The top panel shows the derivative itself; the bottom panel shows the pointwise error.
[7]:
N_vis = 20
# Equidistant (acc=4)
grid_eq = Grid(create_axis(AxisType.EQUIDISTANT, N_vis, -5, 5))
x_eq = grid_eq.coords
df_eq = Diff(grid_eq, 1, 0, acc=4)(f(x_eq))
# Chebyshev
grid_ch = Grid(create_axis(AxisType.CHEBYSHEV, N_vis, -5, 5))
x_ch = grid_ch.coords
df_ch = Diff(grid_ch, 1, 0)(f(x_ch))
# Fine grid for the analytical solution
x_fine = np.linspace(-5, 5, 500)
fig, (ax_top, ax_bot) = plt.subplots(2, 1, figsize=(10, 8),
gridspec_kw={'height_ratios': [3, 2]},
sharex=True)
# -- Top panel: derivative comparison --
ax_top.plot(x_fine, f_prime(x_fine), 'k-', linewidth=2.5, label='Analytical', zorder=5)
ax_top.plot(x_eq, df_eq, 's--', color='#ff7f0e', markersize=6,
label=f'Equidistant FD (acc=4, N={N_vis})')
ax_top.plot(x_ch, df_ch, 'o-', color='#1f77b4', markersize=6,
label=f'Chebyshev (N={N_vis})')
ax_top.set_ylabel(r"$f'(x)$")
ax_top.set_title(f"Numerical vs Analytical Derivative (N = {N_vis})")
ax_top.legend(fontsize=10)
# -- Bottom panel: pointwise error --
ax_bot.semilogy(x_eq, np.abs(df_eq - f_prime(x_eq)), 's--', color='#ff7f0e',
markersize=6, label=f'Equidistant FD (acc=4)')
ax_bot.semilogy(x_ch, np.abs(df_ch - f_prime(x_ch)), 'o-', color='#1f77b4',
markersize=6, label=f'Chebyshev')
ax_bot.set_xlabel("x")
ax_bot.set_ylabel("Pointwise error (abs)")
ax_bot.legend(fontsize=10)
plt.tight_layout()
plt.show()
print(f"Max error with Equidistant FD (acc=4, N={N_vis}): "
f"{np.max(np.abs(df_eq - f_prime(x_eq))):.3e}")
print(f"Max error with Chebyshev (N={N_vis}): "
f"{np.max(np.abs(df_ch - f_prime(x_ch))):.3e}")
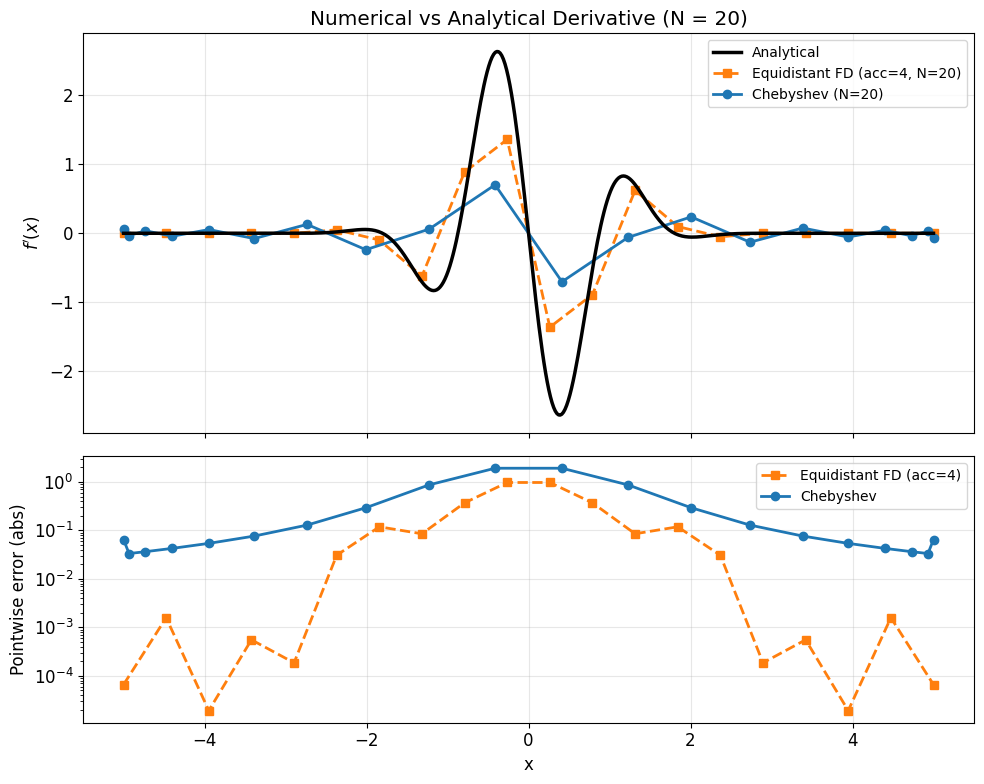
Max error with Equidistant FD (acc=4, N=20): 9.735e-01
Max error with Chebyshev (N=20): 1.916e+00
Summary¶
The results above illustrate a core principle of numerical analysis:
Finite difference methods converge algebraically. Doubling \(N\) reduces the error by a fixed factor (\(2^p\) for a method of order \(p\)). Even with 200 grid points and accuracy order 6, the error remains above \(10^{-8}\).
Chebyshev spectral methods converge exponentially for smooth functions. With just 20 points, the Chebyshev method already achieves errors comparable to what 200+ equidistant finite difference points cannot.
FFT spectral methods are even faster for periodic functions, reaching machine precision as soon as \(N\) exceeds twice the highest frequency in the signal.
The takeaway: 20 Chebyshev points achieve what 200+ equidistant points cannot.
This is why spectral methods are the default choice in numgrids for non-periodic problems.