Getting Started

Installation

pip install --upgrade findiff

For GPU / JAX support, install JAX separately (findiff detects it automatically):

pip install jax          # CPU-only
pip install jax[cuda12]  # NVIDIA GPU

For CuPy support:

pip install cupy-cuda12x

Taking Derivatives

First Derivatives

The first derivative along the 0-th axis (”\(x_0\)-axis”),

\[\frac{\partial}{\partial x_0}\quad,\]

can be defined by

from findiff import Diff

d_dx = Diff(0, dx)

The first argument is the axis along which to take the partial derivative. The second argument is the spacing of the (equidistant) grid along that axis.

Accordingly, the first partial derivative with respect to the k-th axis

\[\frac{\partial}{\partial x_k}\]

is

Diff(k, dx_k)

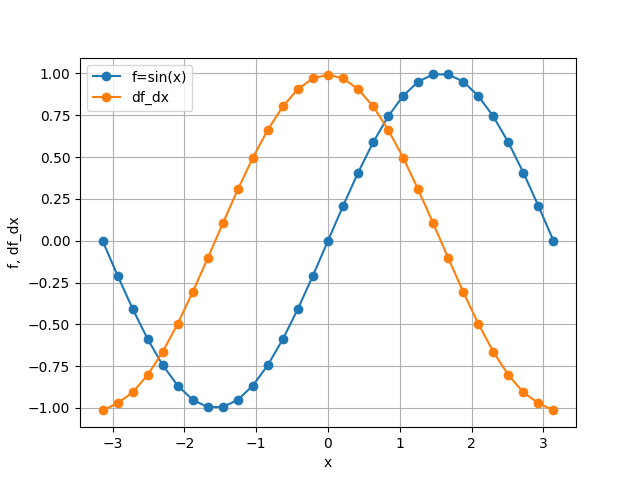
Let’s initialize a one-dimensional array f with some values, for example:

import numpy as np
x = np.linspace(-np.pi, np.pi, 100)
dx = x[1] - x[0]
f = np.sin(x)

Diff objects behave like operators — call them on a numpy ndarray (or a JAX / CuPy array) of any shape:

d_dx = Diff(0, dx)
df_dx = d_dx(f)

Now df_dx is a new array with the same shape as f containing the first derivative with respect to the zeroth axis:

Higher Derivatives

The n-th partial derivative, say with respect to \(x_k\),

\[\frac{\partial^n}{\partial x_k^n}\]

is written by exponentiation:

Diff(k, dx_k) ** n

A mixed partial derivative like

\[\frac{\partial^3}{\partial x^2 \partial y}\]

is written by “multiplication”:

Diff(0, dx)**2 * Diff(1, dy)

General Differential Operators

Diff objects can be combined to describe general differential operators. For example, the wave operator

\[\frac{1}{c^2}\frac{\partial^2}{\partial t^2} - \frac{\partial^2}{\partial x^2}\]

can be written as

1 / c**2 * Diff(0, dt)**2 - Diff(1, dx)**2

if the 0-axis represents the t-axis and the 1-axis the x-axis.

This works both for constant and variable coefficients.

Chaining differential operators is done by multiplication:

\[\left(\frac{\partial}{\partial x} - \frac{\partial}{\partial y}\right) \cdot \left(\frac{\partial}{\partial x} + \frac{\partial}{\partial y}\right) = \frac{\partial^2}{\partial x^2} - \frac{\partial^2}{\partial y^2}\]

or in findiff:

d_dx = Diff(0, dx)
d_dy = Diff(1, dy)

(d_dx - d_dy) * (d_dx + d_dy)

Accuracy Control

By default, findiff uses finite difference schemes with second order accuracy in the grid spacing. Higher orders can be selected with the acc keyword:

Diff(0, dx, acc=4)

for fourth order accuracy.

Finite Difference Coefficients

findiff uses finite difference schemes to calculate numerical derivatives. If needed, the finite difference coefficients can be obtained from the coefficients function, e.g. for the second derivative with second order accuracy:

from findiff import coefficients
coefficients(deriv=2, acc=2)

which yields

{'backward': {'accuracy': 2,
              'coefficients': array([-1.,  4., -5.,  2.]),
              'offsets': array([-3, -2, -1,  0])},
 'center': {'accuracy': 2,
            'coefficients': array([ 1., -2.,  1.]),
            'offsets': array([-1,  0,  1])},
 'forward': {'accuracy': 2,
             'coefficients': array([ 2., -5.,  4., -1.]),
             'offsets': array([0, 1, 2, 3])}}

Matrix Representations

For a given Diff differential operator, you can get a sparse matrix representation using the matrix method:

x = np.linspace(0, 6, 7)
d2_dx2 = Diff(0, x[1] - x[0]) ** 2
u = x**2

mat = d2_dx2.matrix(u.shape)  # returns a scipy sparse matrix
print(mat.toarray())

yields

[[ 2. -5.  4. -1.  0.  0.  0.]
 [ 1. -2.  1.  0.  0.  0.  0.]
 [ 0.  1. -2.  1.  0.  0.  0.]
 [ 0.  0.  1. -2.  1.  0.  0.]
 [ 0.  0.  0.  1. -2.  1.  0.]
 [ 0.  0.  0.  0.  1. -2.  1.]
 [ 0.  0.  0. -1.  4. -5.  2.]]

This also works for general differential operators.

Operators also have eigs and eigsh methods for solving eigenvalue problems directly — see the Matrix Representation guide.

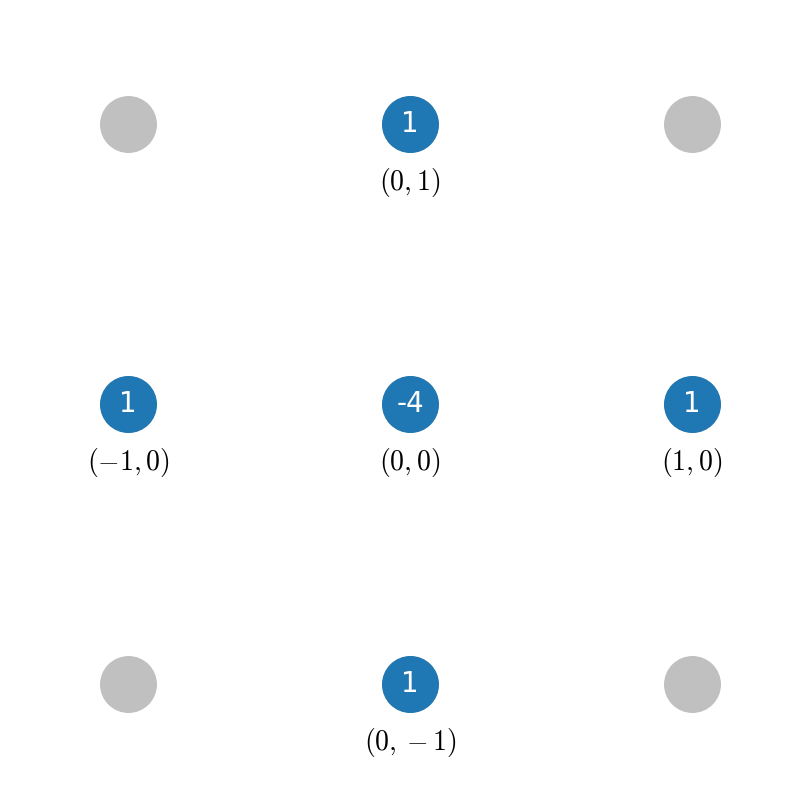
Stencils

Automatic Stencils

When you define a differential operator, findiff automatically chooses suitable stencils to apply on a given grid. For instance, consider the 2D Laplacian

\[\frac{\partial^2}{\partial x^2} + \frac{\partial^2}{\partial y^2}\]

defined (in second order accuracy) as

laplacian = Diff(0, dx) ** 2 + Diff(1, dy) ** 2

When applied, findiff selects the appropriate stencil for each grid point. You can inspect the stencils by calling the stencil method:

laplacian.stencil(f.shape)

In the interior of the grid, the stencil looks like this:

Near the boundaries, findiff automatically switches to asymmetric stencils (of the same accuracy order), for example for a corner:

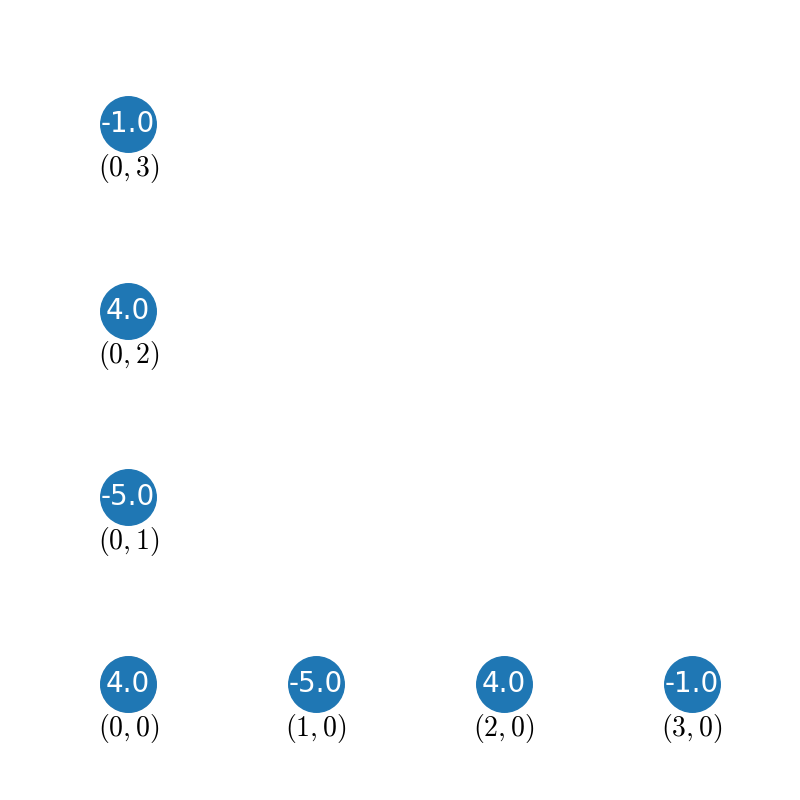
Stencils can also be applied to individual grid points:

x = y = np.linspace(0, 1, 101)
X, Y = np.meshgrid(x, y, indexing='ij')
f = X**3 + Y**3

stencils = laplacian.stencil(f.shape)
stencils.apply(f, (100, 100))  # evaluate at f[100, 100] → 12

Custom Stencils

You can create custom stencils directly using the Stencil class:

from findiff import Stencil

# x-shaped offsets for 2D Laplacian
offsets = [(0, 0), (1, 1), (-1, -1), (1, -1), (-1, 1)]
stencil = Stencil(offsets, {(2, 0): 1, (0, 2): 1})

The second argument defines the derivative operator: {(2, 0): 1, (0, 2): 1} corresponds to \(\frac{\partial^2}{\partial x_0^2} + \frac{\partial^2}{\partial x_1^2}\).

Legacy API

Before version 0.11, the main class was called FinDiff. It is still available for backward compatibility:

from findiff import FinDiff

# equivalent to Diff(0, dx)
d_dx = FinDiff(0, dx, 1)

New code should use Diff instead.